Der initiale Schritt der Sternentstehung ist der Kollaps einer interstellaren Gaswolke. Ob es überhaupt zum Kollaps kommt, entscheidet das Jeans-Kriterium.

Eine insterstellare Molekülwolke befindet sich im Gleichgewicht, wenn sich die nach innen wirkende Gravitationsenergie und der nach außen wirkende Gasdruck ausgleichen. In diesem Zustand ist ein Kollaps und damit auch die Entstehung von Sternen nicht möglich.
Um gravitativ kollabieren zu können, muss eine Molekülwolke eine Reihe von Voraussetzungen erfüllen. Quantitativ beschreiben lassen sich diese Voraussetzungen anhand des Jeans-Kriteriums.
Gemäß dem Jeans-Kriterium kollabiert eine Moleküwolke genau dann, wenn ihre Masse die kritische Jeans-Masse überschreitet.
Die Jeans-Masse gibt also eine Grenzmasse an, oberhalb der sich eine Wolke durch ihre Gravitation zusammenziehen muss.
Die Formel und ihre Bedeutung
Die Jeans-Masse einer Moleküwolke ohne Einwirkung äußerer Kräfte und ohne Drehimpuls kann vereinfacht wie folgt berechnet werden: $$M_{Jeans} = \pi^{\frac{3}{2}} \frac{1}{\sqrt{\rho}} \bigg(\frac{R T}{\mu G}\bigg)^{\frac{2}{3}}$$
Die Formel macht ersichtlich, dass die Jeans-Masse \(M_{Jeans}\) in erster Linie von ihrer Temperatur \(T\), ihrer Dichte \(\rho\) und ihrem Radius \(R\) abhängig ist.
\(\mu\) ist die Masse eines Gasmoleküls, \(G\) ist die Gravitationskonstante.
Für eine Wolke mit höherer Temperatur ist auch die entsprechende Jeans-Masse größer, da sich ein größerer Gasdruck gegen das Gravitationspotenzial richtet. Im Gegensatz dazu wird die Jeans-Masse bei einer höheren Gasdichte kleiner, denn die größere Masse pro Volumen unterstützt einen Kollaps.
Beispiel für verschiedene Parameter
Mit dem folgenden Diagramm lassen sich die Einflüsse von Masse, Temperatur und Dichte leicht ablesen.
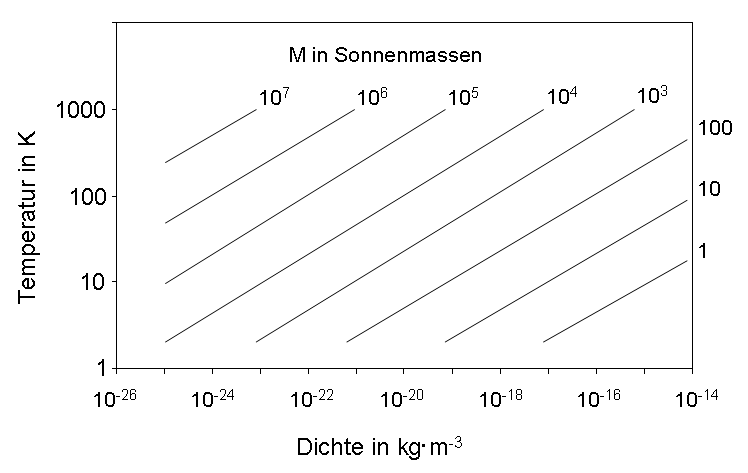
Geht man beispielsweise auf der rechten Seite von einer Masse von 10 Sonnenmassen aus und "wählt" auf der linken Seite eine Temperatur von 10 Kelvin, so lässt sich an der unteren Skala eine Dichte von 10-17 kg × m-3 ablesen.
Weblinks und Einzelnachweise
Hermann Kolanoski: SternentwicklungJürgen Giesen: Entstehung von Sternen
Portal durchsuchen

Protosterne
Nachdem eine Molekülwolke nach ihrem Gravitationskollaps einen prästellaren Kern gebildet hat, bildet sich der Vorläufer eines Sterns: Ein protostellares Objekt oder Protostern.
Der Einfluss von Magnetfeldern auf die Sternentstehung
Anders als zunächst angenommen spielen Magnetfelder eine tragende Rolle bei der Sternentstehung – sie beeinflussen die Geburt von Sternen in mehreren Aspekten.

Kollaps von Molekülwolken
Grundvorausstetzung für die Geburt eines Sterns ist der Kollaps des Sternmaterials. Ob und wie dieser Kollaps zustande kommt, ist von zahlreichen Faktoren abhängig.
